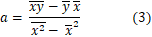很久之前就开始尝试对博客的算法模块进行编写。然而在实际中深深的感觉到门槛陡峭、基础不扎实导致进展缓慢。从“贝叶斯”、“决策树”开始尝试最终选择了经典的最小二乘法作为基础算法理解的开始。在工作期间时间几乎都是碎片化的。对于一些数学理解、公式的解析没有整块的时间十分困难。这部分工作就应该穿插在学校时代的数学学习当中。也希望看到这篇博客的同学尽早确定方向并对一些基础数学和算法部分进行整理和汇总。莫要浅尝辄止知其然而不知所以然。
概念
最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。
思想
简单地说,最小二乘的思想就是要使得观测点和估计点的距离的平方和达到最小.这里的“二乘”指的是用平方来度量观测点与估计点的远近(在古汉语中“平方”称为“二乘”),“最小”指的是参数的估计值要保证各个观测点与估计点的距离的平方和达到最小。在平方和最小时我们认为该估计点为观测点的最优解。从这个上也可以看出,最小二乘也可用于拟合数据模型。
适用问题
曲线拟合、已知一堆点的集合求该集合最适配的函数方程(描述不规范)
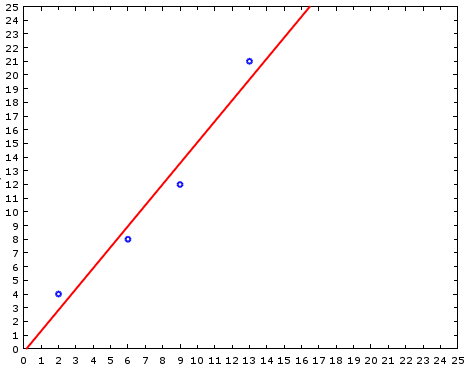
数学解析
就上图而言给定四个观测点我们假设这四个点具有线性关系。
该线性关系可以用等式 y = ax+b 来描述
由最小二乘法的思想来看要找到a和b使得观测点到直线y = ax+b的平方和最小即:
使得: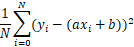 最小
最小
很明显这是一个具有最小值的式子并且在导数为0时取到
令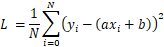
展开:
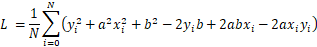
求L关于 a的偏导数
将无关a的项去掉并求导
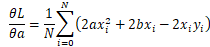
展开
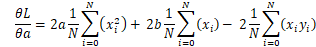
容易看出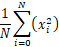 即为x平方的平均值
即为x平方的平均值 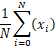 即为x的平均值
即为x的平均值 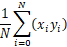 即为x*y的平均值
即为x*y的平均值
用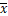 表示
表示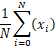
即:
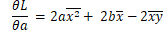
令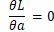 得
得
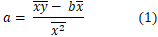
求L关于 b的偏导数
将无关b的项去掉并求导
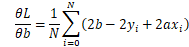
令
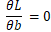 得
得

求得a
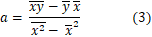
示例
这里使用上面得到的最小二乘法公式对以下数据集进行线性拟合:
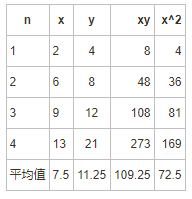
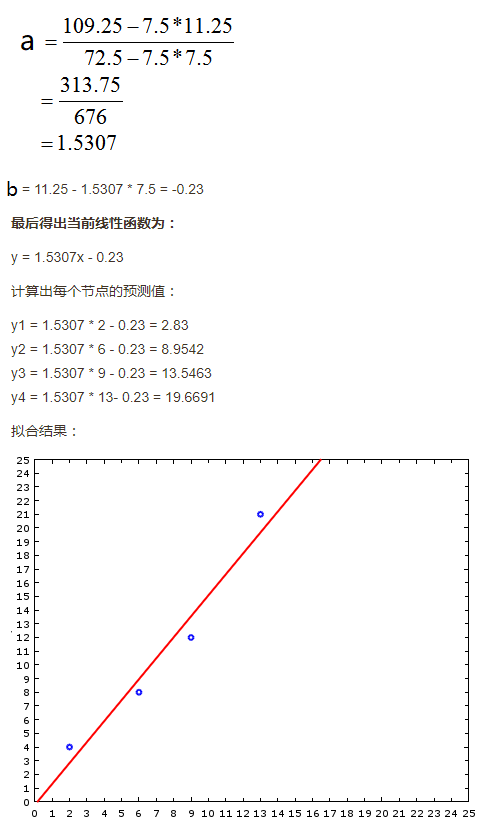
根据上述最小二乘法公式计算出当前数据集最优:a和b
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
| function PolyFit() {
this.polyfit = function (x,y,poly_n,a) {
if(!(x.length >1 && y.length>1))
{
return 2
}
if(x.length!=y.length)
{
return 3
}
for(var i=0;i<x.length;i++)
{
if(isNaN(x[i]) || isNaN(y[i]))
{
return 4
}
}
var i,j;
var tempx = new Array();
var tempy = new Array();
var sumxx = new Array();
var sumxy = new Array();
var ata = new Array();
for(i=0;i<x.length;i++)
{
tempx.push(1);
tempy.push(y[i]);
}
for(i=0;i<2*poly_n+1;i++)
{
for (sumxx[i] = 0, j = 0;j<x.length;j++)
{
sumxx[i] += tempx[j];
tempx[j] *= x[j];
}
}
for (i = 0;i<poly_n + 1;i++)
{
for (sumxy[i] = 0, j = 0;j<x.length;j++)
{
sumxy[i] += tempy[j];
tempy[j] *= x[j];
}
}
for (i = 0;i<poly_n + 1;i++)
{
for (j = 0;j<poly_n + 1;j++)
{
ata[i*(poly_n + 1) + j] = sumxx[i + j];
}
}
this.gauss_solve(poly_n + 1, ata, a, sumxy);
return 1;
}
this.gauss_solve = function(n,A,x,b){
var i, j, k, r;
var max;
for (k = 0;k<n - 1;k++)
{
max = Math.abs(A[k*n + k]);
r = k;
for (i = k + 1;i<n - 1;i++)
{
if (max<Math.abs(A[i*n + i]))
{
max = Math.abs(A[i*n + i]);
r = i;
}
}
if (r != k)
{
for (i = 0;i<n;i++)
{
max = A[k*n + i];
A[k*n + i] = A[r*n + i];
A[r*n + i] = max;
}
}
max = b[k];
b[k] = b[r];
b[r] = max;
for (i = k + 1;i<n;i++)
{
for (j = k + 1;j<n;j++)
{
A[i*n + j] -= A[i*n + k] * A[k*n + j] / A[k*n + k];
}
b[i] -= A[i*n + k] * b[k] / A[k*n + k];
}
}
for (i = n - 1;i >= 0;x[i] /= A[i*n + i], i--)
{
for (j = i + 1, x[i] = b[i];j<n;j++)
{
x[i] -= A[i*n + j] * x[j];
}
}
}
}
|
参考&引用
https://baike.baidu.com/item/%E6%9C%80%E5%B0%8F%E4%BA%8C%E4%B9%98%E6%B3%95/2522346?fr=aladdin
http://bbs.pinggu.org/thread-3041002-1-1.html
http://www.cnblogs.com/softlin/p/5815531.html

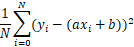 最小
最小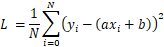
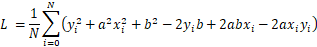
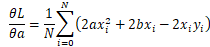
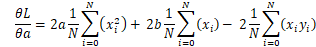
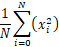 即为x平方的平均值
即为x平方的平均值 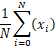 即为x的平均值
即为x的平均值 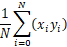 即为x*y的平均值
即为x*y的平均值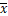 表示
表示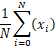
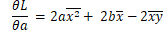
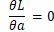 得
得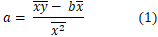
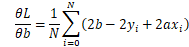
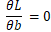 得
得