简介
任何周期性函数,都可以看成不同相位、不同振幅的正弦波的叠加。(误)
(正弦曲线无法组合成一个带有棱角的信号。(例如方波,下文会有图像)但是,我们可以用正弦曲线来非常逼近地表示它,逼近到两种表示方法几乎不存在差别)
应用领域
在信号处理领域,对于一些杂波的滤除,或者特征信号的提取。在时域上可用方法往往不是很多,一些基本的时域滤波算法例如:中值滤波法、限幅法、算数平均法等等多少都会有一定的弊端往往不够通用。这时就需要引入在频域的一些处理算法。而这些算法应用的基础就是将时域信号转化为频域信号。这里需要引入傅里叶变换。如果是转化为时频域信号则需要引入小波变换了。这里只提傅里叶变换。
主要作用
傅里叶变换的主要作用在于将时域图,转化成频域图。根据傅里叶变换的定理我们可以将一副时域图看成是一个周期函数其中的一个周期。
原理
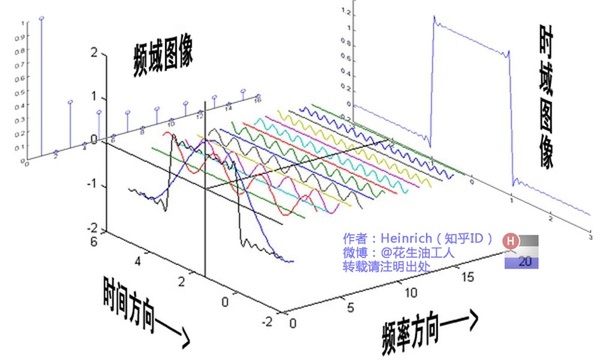


以上三幅图几乎已经将傅里叶变换的原理阐述清楚了。从图一中可以清晰的看到时间维度、频域维度两个维度之间的转化关系。图二清晰的描述了由多个正弦波一步一步叠加为一个方波的过程。图三则是一个动图对于是图二的另一种表达方式引入了公式-图像-叠加图像。
为什么可以进行傅里叶变换
一个时域图像为什么可以转化成频域图像?看到这里你可能会说因为傅里叶变换啊~。(-_-b)但是为什么可以进行傅里叶变换?一个函数为什么可以分解为多个正弦函数的累加?
这里只需要证明若函数f(x)满足一定的条件则
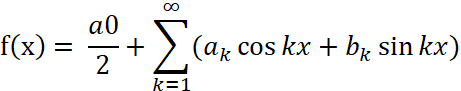
即可证明傅里叶变换成立
证明过程高能链接
弊端
1、傅里叶变换是时域不相关的。若两幅图都是由同样的只是出现顺序不同的频率组成的话,傅里叶变换并不能在频域上区分他们,因为他们在频域上的确是一致的。如下图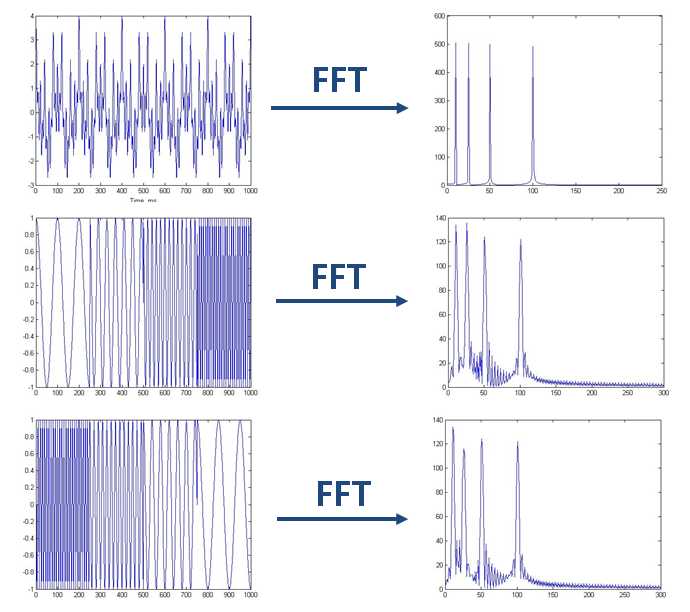
2、采样频率要大于信号频率的两倍。如果采样频域不够则一些高频波可能无法发现。
应用案例
这个滤波算法主要通过,确定杂波信号段、确定特征信号段、将两者时域信号转化为频域信号。用特征信号的频域值减去杂波信号的频域值以实现去除杂波的目的。
提示
本文仅介绍一些基础的概念、原理等。同时受制于作者水平可以说非常非常的粗浅。若想深入理解傅里叶变换算法强烈建议仔细阅读下文的参考及引用。
参考&&引用
https://zhuanlan.zhihu.com/p/19759362
https://zhuanlan.zhihu.com/p/22450818?refer=dong5
https://www.douban.com/note/164400821/
https://baike.baidu.com/item/%E5%82%85%E9%87%8C%E5%8F%B6%E5%8F%98%E6%8D%A2/7119029?fr=aladdin
http://www.baike.com/wiki/%E5%82%85%E9%87%8C%E5%8F%B6%E5%8F%98%E6%8D%A2
http://www.360doc.com/content/13/0328/12/202378_274443797.shtml