牛顿逼近法

简介

牛顿逼近法，又称牛顿法（英语：Newton’s method）又称为牛顿-拉弗森方法（英语：Newton-Raphson method），它是一种在实数域和复数域上近似求解方程的方法。方法使用函数 $f(x)$ 的泰勒级数的前面几项来寻找方程$f(y)=0$的根。

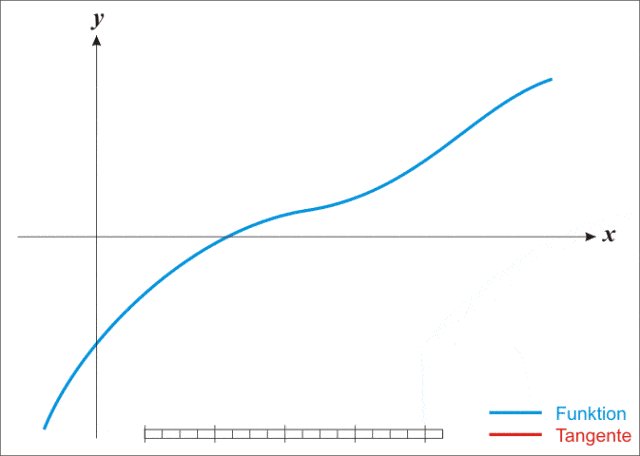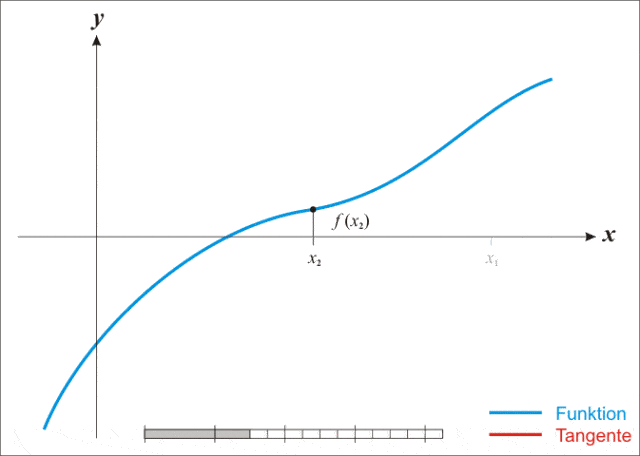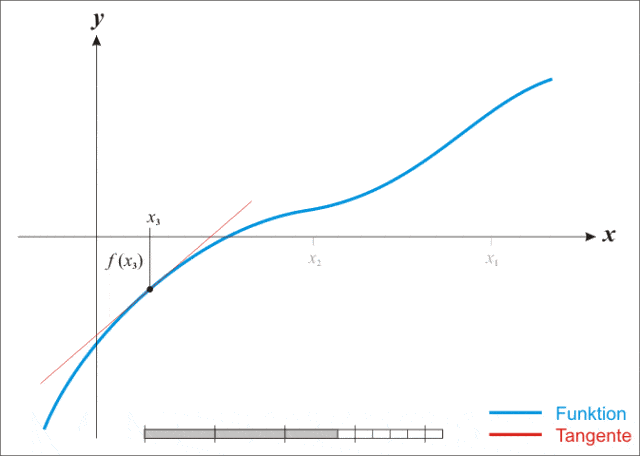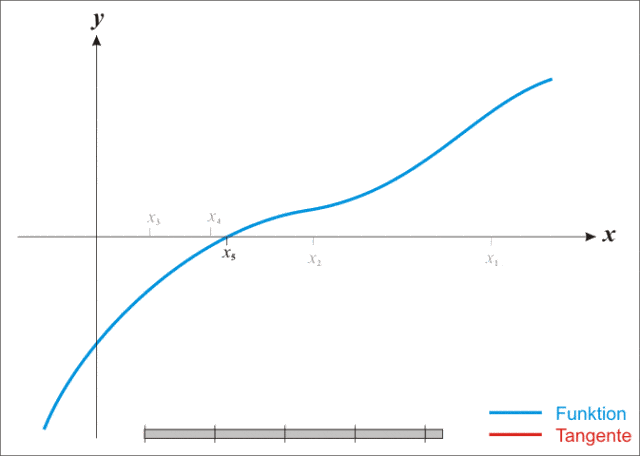
蓝线表示方程$f$而红线表示切线。可以看出$x_{n+1}$比$x_n$更靠近$f$所要求的跟$x$.

首先，选择一个接近函数$f(x)$零点的$x_0$计算相应的$f(x_0)$和切线斜率$f\prime(x_0)$然后我们计算穿过点$(x_0,f(x_0))$并且斜率为$f\prime(x_0)$的直线和x轴的交点坐标，也就是求如下方程的解

$0=(x-x_0)*f\prime(x)+f(x_0)$。

我们将新求的点$x$的坐标明明为$x_1$,通常$x_1$会比$x_0$更接近方程$f(x)=0$的解。因此可以利用$x_1$开始下一轮迭代。迭代公式可化简如下所示：

$x_{n+1} = x_n - {f(x_n) \choose f\prime(x_n)} $

已经证明，如果$f`$是连续的，并且待求的零点x是孤立的，那么在零点周围存在一个区域，只要初始值$x_0$位于这个临近区域内，那么牛顿逼近法必定收敛。

并且，如果$f\prime(x)\neq0$,那么牛顿逼近法将具有平方收敛的性能，粗略的说，没迭代一次，牛顿逼近法结果的有效数字将增加一倍。