凸包算法

背景

凸包算法其实是一个挺常用的算法，例如在这道题(812.最大三角形面积)中，常规的解决方案就是写一个时间复杂度O(N^3)的暴力算法去枚举所有可能出现的三角形，再利用海伦公式去求得三角形面积。不妨我们大胆假设，在一堆点的集合中，其中面积最大的三角形的顶点，必然位于这些点的凸包上。论证我们先跳过，直接用结果去验证假设是否成立(经验证，假设是成立的)

简介

凸包算法有很多种，例如

Graham扫描法 nlogn
Jarvis步进法 nH (H为凸包上的点最差情况会退化成 n^2)
分治法 nlogn
穷举法 n^3 (两点确定一条直线，如果剩余的其它点都在这条直线的同一侧，则这两个点是凸包上的点，否则就不是)
Melkman算法 (基于双向链表来做的，具体没看懂)

这里详细介绍常规的 Graham扫描法,Graham扫描法时间复杂度优于Jarvis步进法，理解起来稍微比之困难一些，但影响不大。

执行逻辑

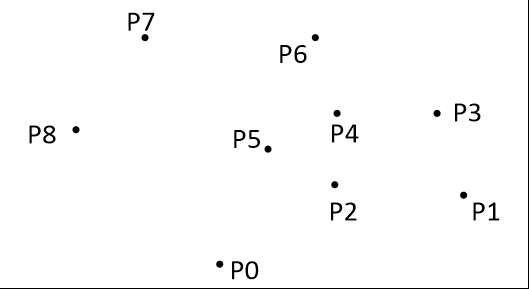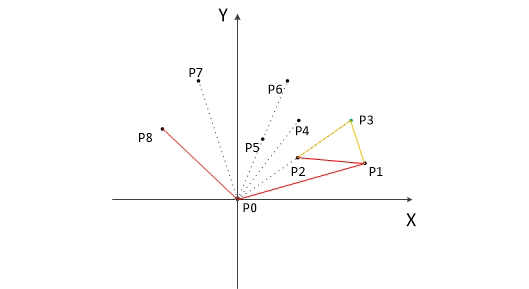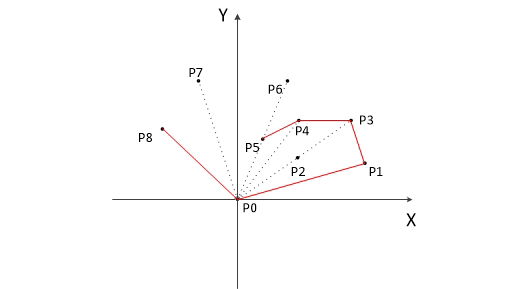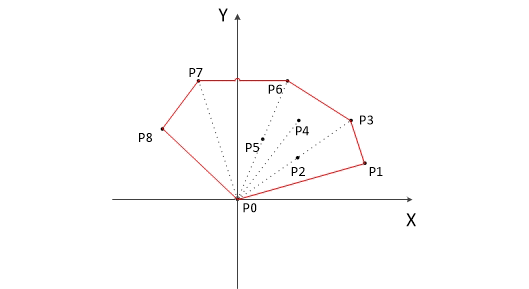
把所有点放在二维坐标系中，则纵坐标最小的点一定是凸包上的点，如图中的P0。
计算各个点相对于 P0 的幅角 α ，按从小到大的顺序对各个点排序。(这里涉及到一个极角排序算法)
其中最左边的点，和最右边的点肯定为凸包上的点。根据p8,p0,p1构建凸包栈[p8,p0,p1]
判断凸包栈的栈顶两个元素(这里为[p0,p1]直线记作L0-1)构建的执行和凸包栈的栈顶元素与当前点构成的直线(这里为[p1,p2]直线记作L1-2)
判断L1-2在L0-1的左侧还是右侧还是线上，如果在直线右边跳转步骤7，如果在直线上或者直线坐标跳转步骤6
当前点是凸包上的点，把它压入栈，跳转步骤4开始判断下一个节点。
如果L1-2在L0-1的右边即p1不是凸包上的点p1出栈跳转步骤4（由于p1点是起始点，所以不存在[L1-2在L0-1的右边]的情况这里仅举例,在上图中可以看L4-5和L4-6,L4-6在L4-5的右边，即p4出栈）
判断当前点是否是顶点集合的最后一个点即p8,是则退出循环。

代码

// 这里仅作算法说明作用，实现并不规范
const getConvexHull = function(points) {
// 计算叉积
function cross(x0, y0, x1, y1) {
return x0 * y1 - x1 * y0;
}
// 计算极角
function crossAngle(p0, p1, p2) {
return cross(p1[0] - p0[0], p1[1] - p0[1], p2[0] - p0[0], p2[1] - p0[1]);
}
// 极角排序
function sortCmp(p1, p2) {
return crossAngle(p0, p1, p2);
    }
    // 获取p0点
let p0 = points[0];
for (let i = 1; i < points.length; i++) {
if (points[i][1] < p0[1] || (points[i][1] === p0[1] && points[i][1] < p0[1])) {
p0 = points[i];
}
    }
    // 顶点排序
points.sort(sortCmp);
    
    // 从顶点序列中 剔除p0点
if (points[0] === p0) {
points.shift();
}
if (points[points.length - 1] === p0) {
points.pop();
    }
    
let firstNode = points.pop();
let lastNode = undefined;
let convexHull = undefined;
lastNode = points[0];
convexHull = [ lastNode, p0, firstNode ];

for (let i = points.length - 1; i >= 0; i--) {
        // 判断是不是在线的右边
while (crossAngle(convexHull[convexHull.length - 2], convexHull[convexHull.length - 1], points[i]) < 0) {
            // 在右边即上一个点不是凸包上的点 出栈
convexHull.pop();
        }
        // 当前点入栈
convexHull.push(points[i]);
    }
    // TODO fixme 
    // 多压入最有一个顶点时退出该点
if (convexHull[0] === convexHull[convexHull.length - 1]) {
convexHull.pop();
}
return convexHull;
};

参考 & 引用

https://baike.baidu.com/item/%E5%87%B8%E5%8C%85/179150?fr=aladdin

https://www.cnblogs.com/aiguona/p/7232243.html

https://visualgo.net/zh/convexhull

https://www.cnblogs.com/cglongge/p/9408417.html