公交车概率论问题

怕不是上了个假大学系列第一篇。

问题

公交车站有两趟公交车、A五分钟一趟、B十分钟一趟。问在该公交车站一分钟内等到车的概率。

答案

0.28

复习

举个掷骰子的例子简单回顾一下基本概念

一个可以掷出1到6的骰子，随机投掷一次获得偶数点数的概率是多少？

很简单的，从事件与样本的角度来说，随机投掷一次骰子是作为一种随机试验，它简单满足三个条件：

1. 可以被重复；
2. 具有多种可能结果并均明确可知；
3. 试验结果不可预先获知。

而我们将骰子可能出现的每一种结果称为样本点，样本点是一种单例，换言之，它的结果是单一而不可再分解的，每一个样本点都彼此不相容，因而它是构成试验结果的最基础原子，故而样本点也被称为基本事件。

而所有样本点（也即所有的可能结果）的集合就被称为样本空间，亦或者可以说所有的基本事件组成的集合称为基本事件空间，记作：
$$
\Omega = {1,2,3,4,5,6}
$$
接着，我们可以将一次试验可能出现的结果称为随机事件，例如例子中的骰子为偶数点数就是一个随机事件，可使用大写字母记为：
$$
A = {骰子点数为偶数} = {2,4,6}
$$
于是，自然的，便可以计算，事件$A$的概率即事件$A$所包含的可能结果占所有可能结果的比例，为：
$$
P(A) = \frac {3}{6} = \frac {1}{2}
$$

解题

计算法

该题公交车A的样本空间为$\Omega = [0,5)$,随机事件为$\Omega = [0,1)$，等到公交车A的概率为

$$
P(A) =\frac {[0,1)}{[0,10)} = \frac {1}{10}
$$

该题公交车B的样本空间为$\Omega = [0,10)$,随机事件为$\Omega = [0,1)$等到公交车B的概率为
$$
P(B) =\frac {[0,1)}{[0,5)} = \frac {1}{5}
$$

因为在一分钟内公交车A和B有可能同时到达，直接计算能等到公交车的概率相对比较复杂，我们可以计算一分钟内没有遇到任何公交车的概率，除去一分钟内没有遇到任何公交车的概率即为一分钟内遇到公交车的概率：

$$
P(遇到公交车) = 1 - \frac{9}{10} * \frac{4}{5} = 0.28
$$

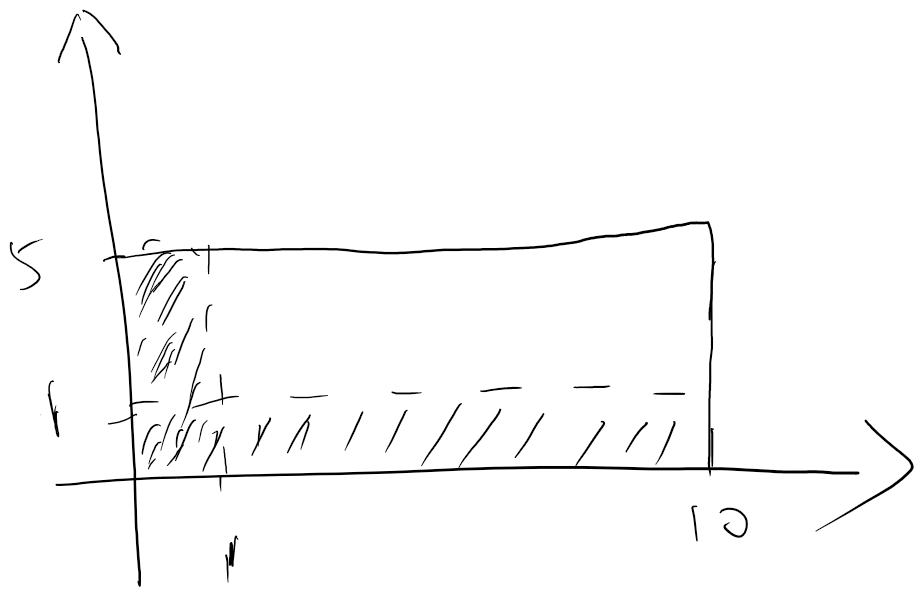
作图法

如图，整个矩形可表示整个样本空间，阴影部分即为等到公交车事件。以面积比例来算即为$1-0.9*0.8 = 0.28$