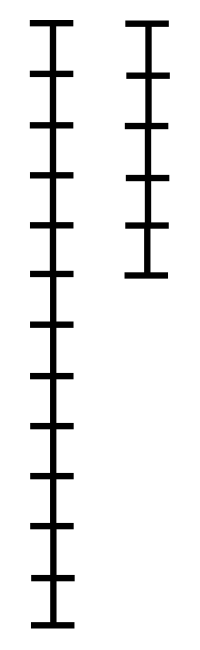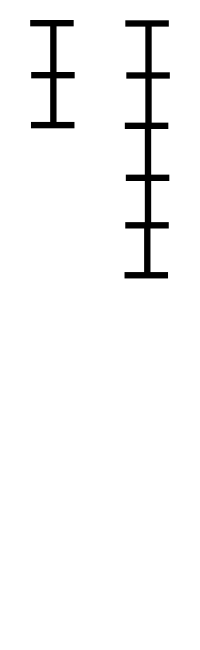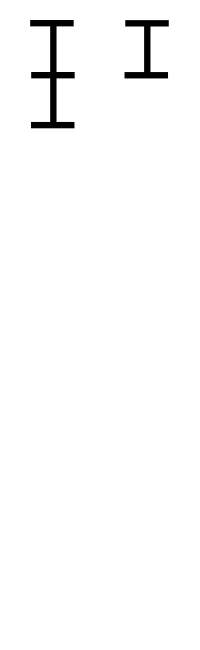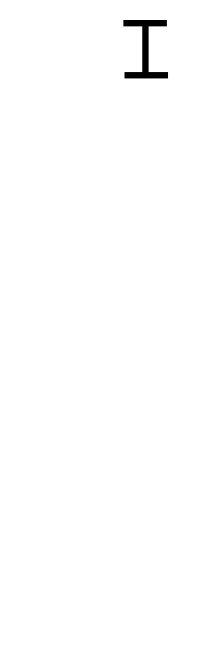辗转相除法求最大公约数
怕不是上了个假大学系列第二篇。
问题
求252和105的最大公约数。
答案
21
复习
最大公约数:两个整数的最大公约数是能够同时整除它们的最大的正整数。
辗转相除法: 两个正整数a和b(a>b),它们的最大公约数等于a除以b的余数c和b之间的最大公约数。
解题
1
2
3
4
5
6
| 252 mod 105 = 42
105 mod 42 = 21
42 mod 21 = 0
令求最大公约数方法为f(a,b)即:
f(252,105) = f(105,42) = f(42,21) = 21
|
理解
1
2
3
4
5
6
7
8
9
| 步骤1 252 mod 105 = 42
步骤2 105 mod 42 = 21
步骤3 42 mod 21 = 0
步骤1即在尝试判断105是不是252的最大公约数,由于有余数42即105不是252的最大公约数。
由于252对105取模即除去余数后的值(252-42=210)必然能整除105。
由以上原因即可以将问题转化为求105和42的最大公约数。(105能整除105,252-42能整除105,假设105和42的最大公约数为X即252和105肯定能整除X)以此逐渐迭代即可求得252和105的最大公约数。
|
动画说明
辗转相除法的演示动画:两条线段长分别可表示252和105,则其中每一小分段长代表最大公约数21。如动画所示,只要辗转地从大数中减去小数,直到其中一段的长度为0,此时剩下的一条线段的长度就是252和105的最大公因数。
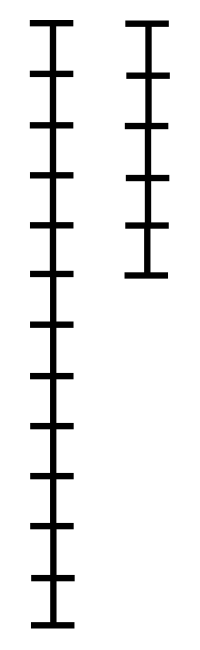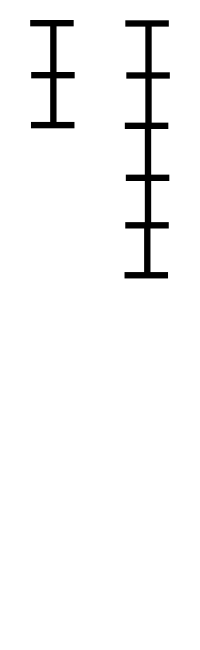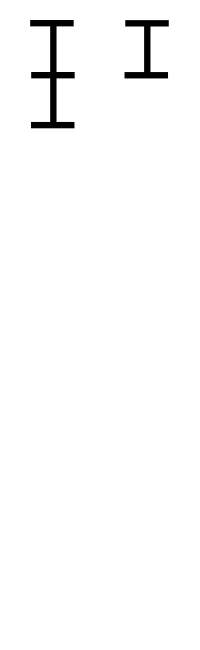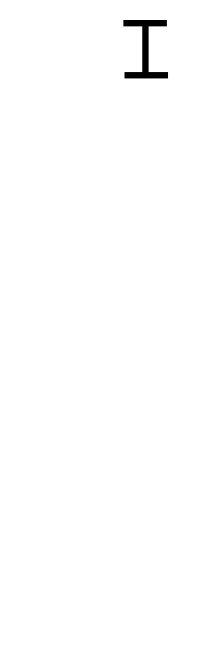
参考 & 引用
辗转相除法 - 维基百科,自由的百科全书 (wikipedia.org)
漫画算法:辗转相除法是什么鬼? - 知乎 (zhihu.com)