SZ 博客

忠于理想 忠于技术

0%

BigO

发表于 分类于 阅读次数：

算法的复杂度通常会使用BigO来表述，但会相对比较抽象，本文会结合算法实例以及图像相对具象的去表述时间复杂度这个概念。

BigO主要有以下几种表达式来描述时间复杂度：

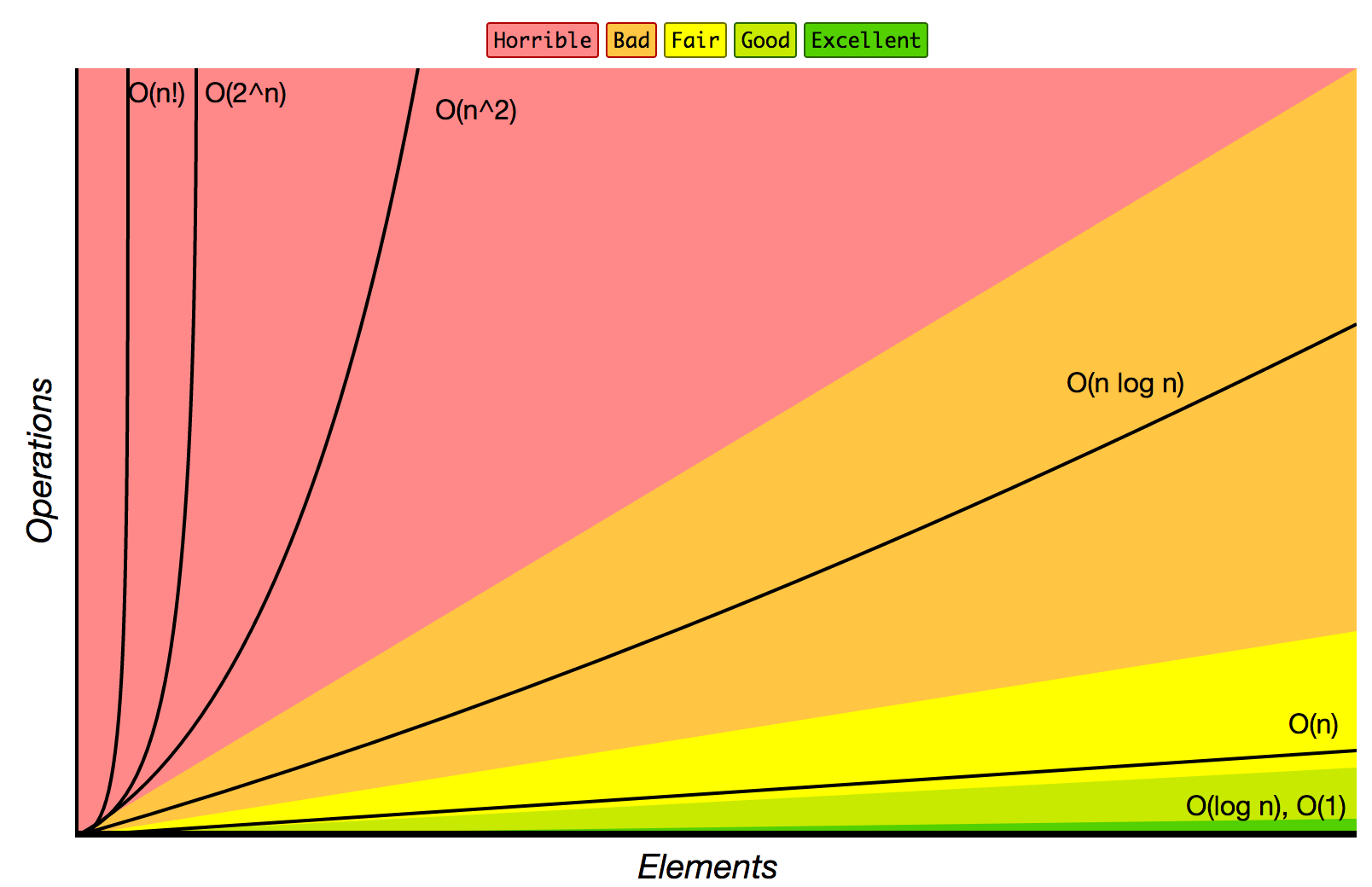
  • O(1)：常量时间
  • O(n)：线性时间
  • O(log n)：对数时间
  • O(n^2)：二次方时间
  • O(2^n)：指数时间
  • O(n!)：阶乘时间

每种时间复杂度有所不同，下面我们一起来详细了解这几种时间复杂度。

算法复杂度和大O表示法 - 莫邪

示例及测试

以题目338. 比特位计数为例，简单使用几种不同复杂度的方案实现，以测试具体耗时。

给你一个整数 n ，对于 0 <= i <= n 中的每个 i ，计算其二进制表示中 1 的个数 ，返回一个长度为 n + 1 的数组 ans 作为答案。

O(1)

打表法, 所有数据均已计算，直接返回结果。时间复杂度O1

1
2
3
4
5
6
7
8
9
10
const answer = [
  0, 1, 1, 2, 1, 2, 2, 3, 1, 2, 2, 3, 2, 3, 3, 4, 1, 2, 2, 3, 2, 3, 3, 4, 2, 3,
  3, 4, 3, 4, 4, 5, 1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5, 2, 3, 3, 4,
  3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6, 1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4,
  4, 5, 2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6, 2, 3, 3, 4,
];

const countBits = function (n) {
  return answer.slice(0, n + 1);
};

O(n)

动态规划，以当前值的计算结果作为输入通过一次计算得到下一个值的计算结果。

1
2
3
4
5
6
7
8
9
10
11
12
const countBits = function (n) {
  const result = [0, 1];
  if (n <= 1) return result.slice(0, n + 1);
  for (let i = 2; i <= n; i++) {
    if (i % 2 === 0) {
      result.push(result[i / 2]);
    } else {
      result.push(result[i - 1] + 1);
    }
  }
  return result;
};

O(nlogn)

动态规划，以当前值的计算结果作为输入通过一次计算得到下一个值的计算结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
const countBits = function(n) {
    const bits = new Array(n + 1).fill(0);
    // 一次循环 n
    for (let i = 0; i <= n; i++) {
        // log n
        bits[i] = countOnes(i);
    }
    return bits
};
// Brian Kernighan 算法(log n)
// 当数值为 10 时会进行两次运算，当数值为 100 时会进行三次运算，当数值为 1000 时会进行六次运算， 呈对数关系。
const countOnes = (x) => {
    let ones = 0;
    while (x > 0) {
        x &= (x - 1);
        ones++;
    }
    return ones;
}

耗时统计

这里纵向对比各算法策略的耗时，countBits(100)计算次数与耗时的统计表格如下单位(毫秒)

计算次数 O(1) O(n) O(nlogn)
10 0.048095703125 0.294189453125 0.534912109375
100 0.093017578125 2.208984375 0.626953125
1000 0.1787109375 2.641845703125 1.37890625
10000 2.102294921875 15.5888671875 9.111083984375
100000 9.434814453125 36.311279296875 45.73291015625
1000000 34.5498046875 261.041015625 438.174072265625