起源于这道题:371.两整数之和复习下二进制加法内容几乎照搬位运算详解
题目说不能使用运算符 + 和 -,那么我们就要使用其他方式来替代这两个运算符的功能。
jsonp本质上是利用<script>不受同源策略限制的特性,创建一个回调函数,然后在远程服务上调用这个函数并且将JSON 数据形式作为参数传递,完成回调。
将JSON数据填充进回调函数,这就是JSONP的JSON+Padding的含义。
好像一张图就够了
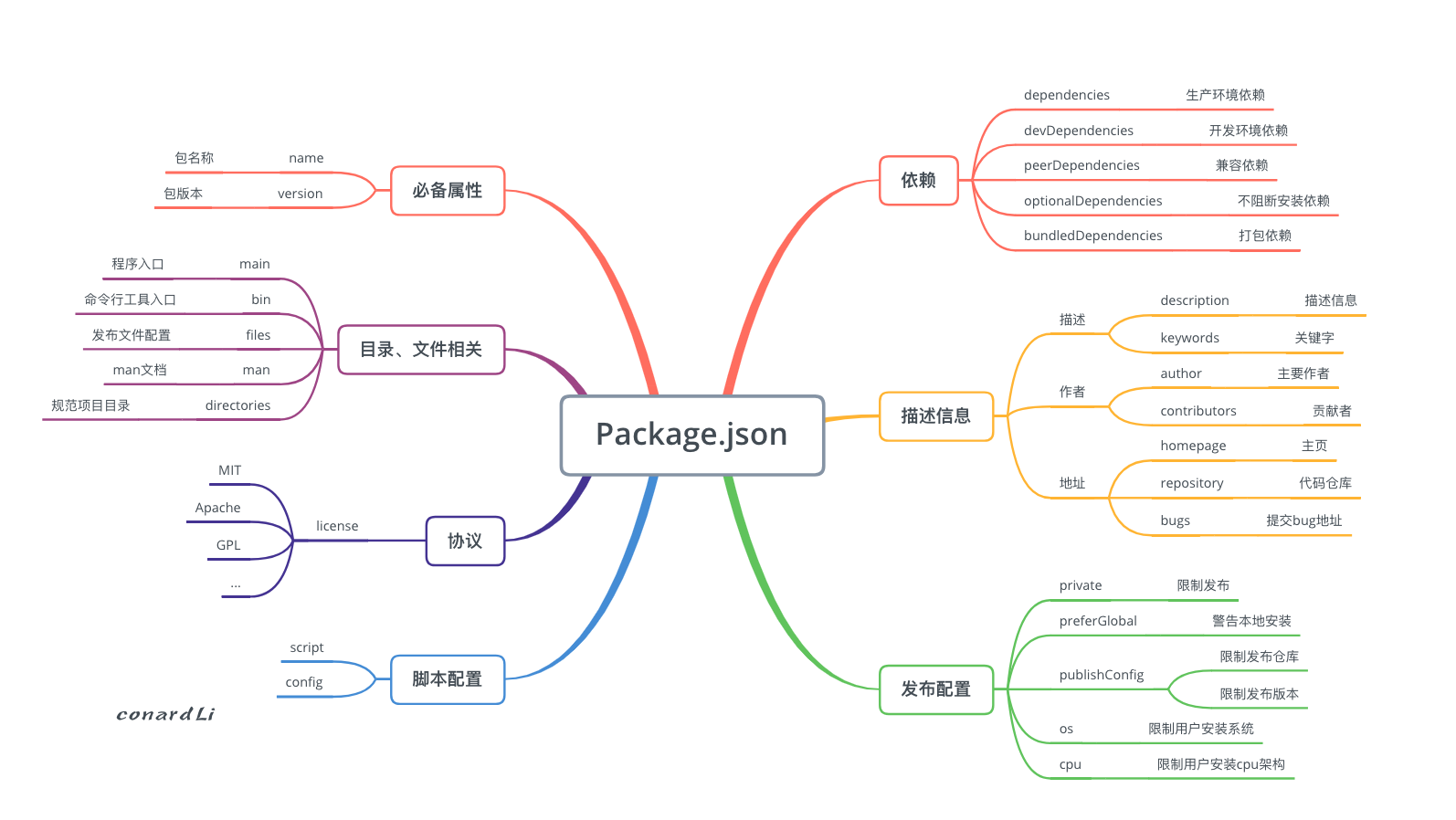
[http://www.conardli.top/blog/article/%E5%89%8D%E7%AB%AF%E5%B7%A5%E7%A8%8B%E5%8C%96/%E5%89%8D%E7%AB%AF%E5%B7%A5%E7%A8%8B%E5%8C%96%EF%BC%88%E4%BA%8C%EF%BC%89package.json%E7%9F%A5%E5%A4%9A%E5%B0%91%EF%BC%9F.html# %E5%BF%85%E5%A4%87%E5%B1%9E%E6%80%A7](http://www.conardli.top/blog/article/前端工程化/前端工程化(二)package.json知多少?.html# 必备属性)
npm包 中的模块版本都需要遵循 SemVer规范——由 Github 起草的一个具有指导意义的,统一的版本号表示规则。实际上就是 Semantic Version(语义化版本)的缩写。
SemVer规范官网:https://semver.org/
cookie存在浏览器本地,不设置失效时间的话存在内存中,而不是硬盘。大小限制在4k每次请求都会携带cookie。一般用于存储一些登录、或权限信息。
session存在服务端,客户端无法访问其信息。通过seesion id和seesion内容做映射。由于在服务端集中存储,当用户庞大时、不易做分布式扩展。需要单独的认证服务器。
webstorage存在浏览器本地,大小一般为5M,请求不会携带webstorage内部的信息。必要的信息需要从webstorage获取写入ajax请求传递。
不管什么程序语言,内存生命周期基本是一致的:
所有语言第二部分都是明确的。第一和第三部分在底层语言中是明确的,但在像JavaScript这些高级语言中,大部分都是隐含的。
值的初始化
为了不让程序员费心分配内存,JavaScript 在定义变量时就完成了内存分配。
1 | var n = 123; // 给数值变量分配内存 |
通过函数调用分配内存
有些函数调用结果是分配对象内存:
1 | var d = new Date(); // 分配一个 Date 对象 |
有些方法分配新变量或者新对象:
1 | var s = "azerty"; |
使用值
使用值的过程实际上是对分配内存进行读取与写入的操作。读取与写入可能是写入一个变量或者一个对象的属性值,甚至传递函数的参数。
当内存不再需要使用时释放
大多数内存管理的问题都在这个阶段。在这里最艰难的任务是找到“哪些被分配的内存确实已经不再需要了”。它往往要求开发人员来确定在程序中哪一块内存不再需要并且释放它。
高级语言解释器嵌入了“垃圾回收器”,它的主要工作是跟踪内存的分配和使用,以便当分配的内存不再使用时,自动释放它。这只能是一个近似的过程,因为要知道是否仍然需要某块内存是无法判定的(无法通过某种算法解决)。
如上文所述自动寻找是否一些内存“不再需要”的问题是无法判定的。因此,垃圾回收实现只能有限制的解决一般问题。本节将解释必要的概念,了解主要的垃圾回收算法和它们的局限性。
垃圾回收算法主要依赖于引用的概念。在内存管理的环境中,一个对象如果有访问另一个对象的权限(隐式或者显式),叫做一个对象引用另一个对象。例如,一个Javascript对象具有对它原型的引用(隐式引用)和对它属性的引用(显式引用)。
在这里,“对象”的概念不仅特指 JavaScript 对象,还包括函数作用域(或者全局词法作用域)。
这是最初级的垃圾收集算法。此算法把“对象是否不再需要”简化定义为“对象有没有其他对象引用到它”。如果没有引用指向该对象(零引用),对象将被垃圾回收机制回收。
1 | var o = { |
限制:循环引用
该算法有个限制:无法处理循环引用的事例。在下面的例子中,两个对象被创建,并互相引用,形成了一个循环。它们被调用之后会离开函数作用域,所以它们已经没有用了,可以被回收了。然而,引用计数算法考虑到它们互相都有至少一次引用,所以它们不会被回收。
1 | function f(){ |
实际例子
IE 6, 7 使用引用计数方式对 DOM 对象进行垃圾回收。该方式常常造成对象被循环引用时内存发生泄漏:
1 | var div; |
在上面的例子里,myDivElement 这个 DOM 元素里的 circularReference 属性引用了 myDivElement,造成了循环引用。如果该属性没有显示移除或者设为 null,引用计数式垃圾收集器将总是且至少有一个引用,并将一直保持在内存里的 DOM 元素,即使其从DOM 树中删去了。如果这个 DOM 元素拥有大量的数据 (如上的 lotsOfData 属性),而这个数据占用的内存将永远不会被释放。
这个算法把“对象是否不再需要”简化定义为“对象是否可以获得”。
这个算法假定设置一个叫做根(root)的对象(在Javascript里,根是全局对象)。垃圾回收器将定期从根开始,找所有从根开始引用的对象,然后找这些对象引用的对象……从根开始,垃圾回收器将找到所有可以获得的对象和收集所有不能获得的对象。
这个算法比前一个要好,因为“有零引用的对象”总是不可获得的,但是相反却不一定,参考“循环引用”。
从2012年起,所有现代浏览器都使用了标记-清除垃圾回收算法。所有对JavaScript垃圾回收算法的改进都是基于标记-清除算法的改进,并没有改进标记-清除算法本身和它对“对象是否不再需要”的简化定义。
循环引用不再是问题了
在上面的示例中,函数调用返回之后,两个对象从全局对象出发无法获取。因此,他们将会被垃圾回收器回收。第二个示例同样,一旦 div 和其事件处理无法从根获取到,他们将会被垃圾回收器回收。
限制: 那些无法从根对象查询到的对象都将被清除
尽管这是一个限制,但实践中我们很少会碰到类似的情况,所以开发者不太会去关心垃圾回收机制。
https://developer.mozilla.org/zh-CN/docs/Web/JavaScript/Memory_Management
webpack的主要工作是将模块打包,这些模块可能包括js代码模块,css模块,一些其他静态资源等。无论是在pro模式下还是在dev模式下本质上都是将模块打包成资源,并依赖一些插件依照一些规范对这些资源进行一定的工程化整合,解决一些前端开发、部署的公共性问题。使其成为一个开发或者构建的封闭实体。
就开发过程而言一般需要一个开发服务器(WebpackDevServer)、一个代码解析器(babel)(ES6或Ts代码需要转化为es5 js代码),一个资源整合器(webpack)。
整体流程上相对比较简单,根据webpack的config生成webpack,根据WebpackDevServer的config生成WebpackDevServer,监听端口和host,启动服务,主体流程就算走完。