CRA应用部署到服务器子目录
CRA应用部署二级路由问题
BrowserRouter 路由basename写入window.location.pathname
1 | function App() { |
react-router 二级路由直接访问404问题解决
JS语法糖
三维力学图布局算法-Force Layout 3D
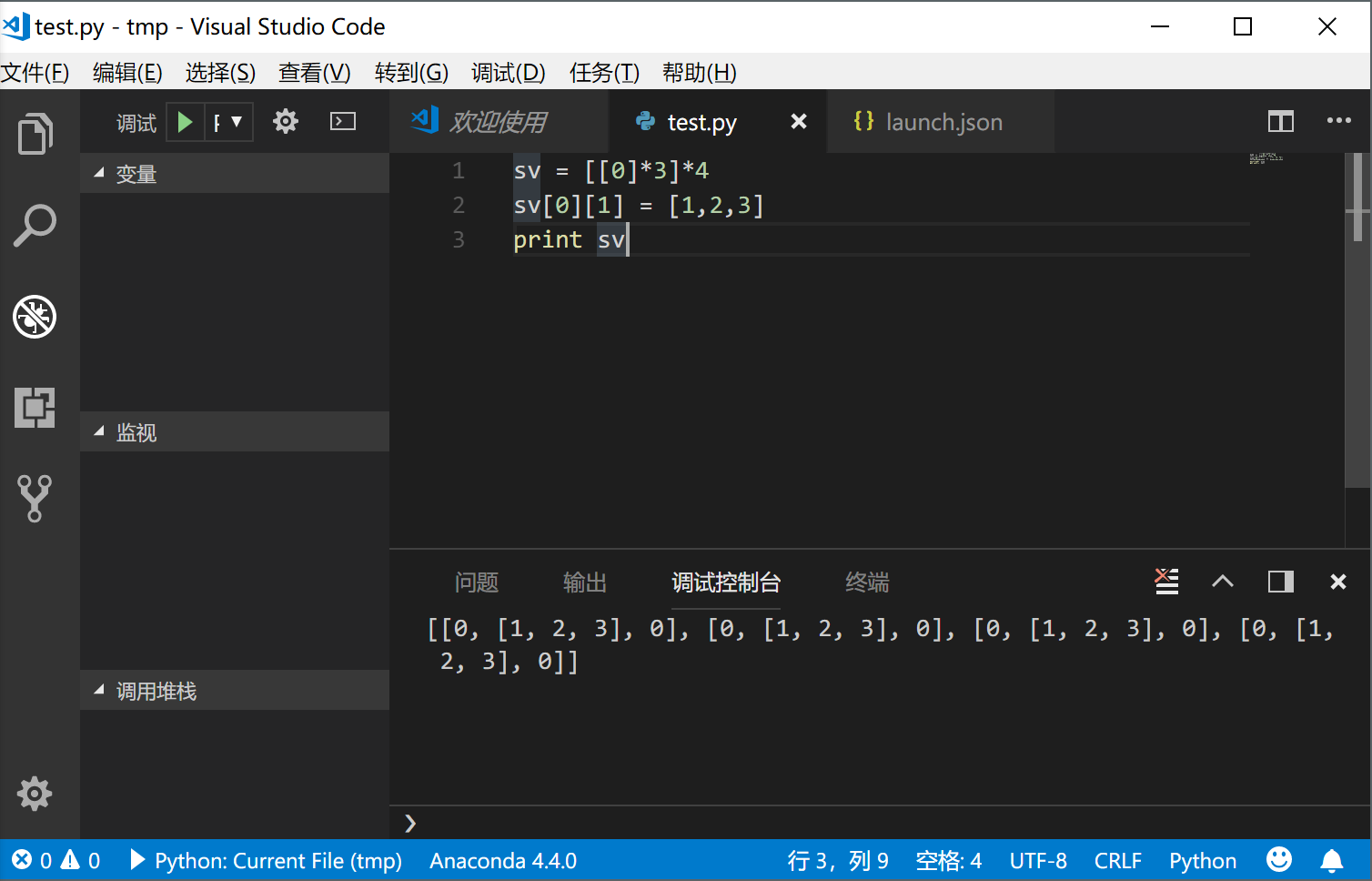
Python数组指针
console的几种写法
全站HTTPS之路
硬件的性能比例
桌面电脑显卡天梯图
http://www.mydrivers.com/zhuanti/tianti/gpu/
桌面电脑CPU天梯图
http://www.mydrivers.com/zhuanti/tianti/cpu/
笔记本电脑显卡天梯图
http://www.mydrivers.com/zhuanti/tianti/gpum/
笔记本电脑CPU天梯图
http://www.mydrivers.com/zhuanti/tianti/cpum/
移动设备CPU天梯图
http://www.mydrivers.com/zhuanti/tianti/01
服务器CPU天梯图
https://www.cpubenchmark.net/high_end_cpus.html